To iterate is Human, to recurse divine.

——Laurence Peter Deutsch

递归的概念

递归（Recursion），在数学和计算机科学中，是指在函数的定义中使用函数自身的方法。

递归的实现主要包含两个过程：

  • 递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。

  • 归：触发终止条件后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

递归三步走：

  1. 写出递推公式：找到将原问题分解为子问题的规律，并且根据规律写出递推公式。
  2. 明确终止条件：推敲出递归的终止条件，以及递归终止时的处理办法。
  3. 将递推公式和终止条件翻译成代码。

递归函数的一般代码形式：

1
2
3
4
def func(传入数值):
    if 终止条件:
        return 最小子问题解
    return func(缩小规模)

如何理解递归

简单例子

计算n!n!。

其代码实现如下：

1
2
3
4
def factorial(n):
    if n == 1:
        return 1
    return n * factorial(n-1)

最好的理解这个递归过程的办法就是把式子展开：

\begin{split}&f(6) \\ &= 6 * f(5) \\ &= 6 * (5 * f(4)) \\ &= 6 * (5 * (4 * f(3))) \\ &= 6 * (5 * (4 * (3 * f(2))) \\ &= 6 * (5 * (4 * (3 * (2 * f(1))))) \\ &= 6 * (5 * (4 * (3 * (2 * 1))) \\ &= 6 * (5 * (4 * (3 * 2) \\ &= 6 * (5 * (4 * 6) \\ &= 6 * (5 * 24) \\ &= 6 * 120 \\ &= 720 \end{split}

先递进，再回归，这就是递归。

树递归

对于任何递归问题，都可以画一个递归树，显示每一层的递归调用及其关系。

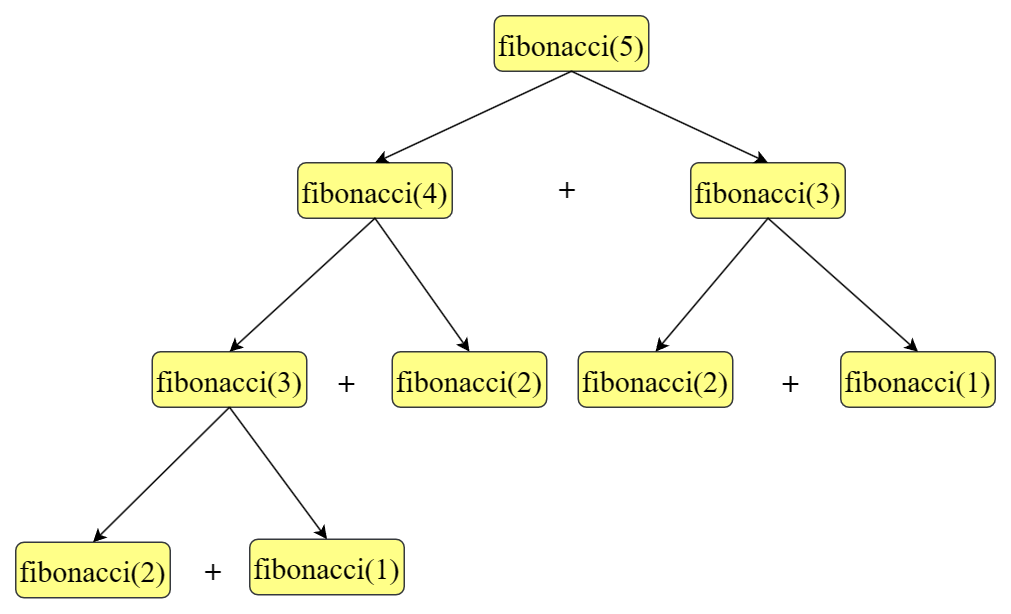
给定一个斐波那契数列0,1,1,2,3,5,8,13,...0,1,1,2,3,5,8,13,...，求该数列的第nn个数字。

设斐波那契数列的第nn个数字为f(n)f(n)，易得下面两个结论：

  1. 数列的前两个数字为f(1)=0f(1) = 0和f(2)=1f(2) = 1。
  2. 数列中的每个数字是前两个数字的和，即f(n)=f(n−1)+f(n−2)f(n)=f(n-1) + f(n-2)。

根据这两个结论，我们可以得到递归公式：

f(n)={0n=11n=2f(n−1)+f(n−2)n>2f(n) = \left\{\begin{matrix} 0 & n=1 \\ 1 & n=2 \\ f(n-1) + f(n-2) & n > 2 \end{matrix}\right.

书写其简单代码为：

1
2
3
4
5
6
7
def fibonacci(n):
    if n == 1:
        return 0
    elif n == 2:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

根据这个递归公式，以计算fibonacci(4)为例可以画出递归树：

理解调用栈

在程序执行中，递归是利用堆栈来实现的。每一次递推都需要一个栈空间来保存调用记录，每当进入一次函数调用，栈空间就会加一层栈帧。每一次回归，栈空间就会减一层栈帧。由于系统中的栈空间大小不是无限的，所以，如果递归调用的次数过多，会导致栈空间溢出。

递归的应用

在 力扣（LeetCode）平台上有专项的递归算法练习题目：递归 - 力扣 (LeetCode)

参考资料